拓扑游戏解法,探索无限连接的奥秘

亲爱的读者们，今天我要带你们走进一个充满奇思妙想的数学世界，探索一种叫做“拓扑游戏解法”的神奇技巧。想象你手中有一张错综复杂的地图，上面布满了各种路径和节点，而你，就是那个要在这张地图上找到最优路径的探险家。准备好了吗？让我们开始这场数学之旅吧！

一、拓扑世界的初探

在数学的海洋里，有一个叫做“拓扑学”的分支，它研究的是几何形状在连续变形下保持不变的性质。听起来是不是有点抽象？别急，让我用一个简单的例子来解释。

想象你有一个咖啡杯和一个甜甜圈，虽然它们的形状看起来完全不同，但在拓扑学家的眼中，它们是等价的。因为你可以通过连续的变形（比如拉伸、压缩、扭曲）将一个变成另一个，而不需要切割或撕裂。这种性质在拓扑学中被称为“同胚”。

二、拓扑游戏解法的诞生

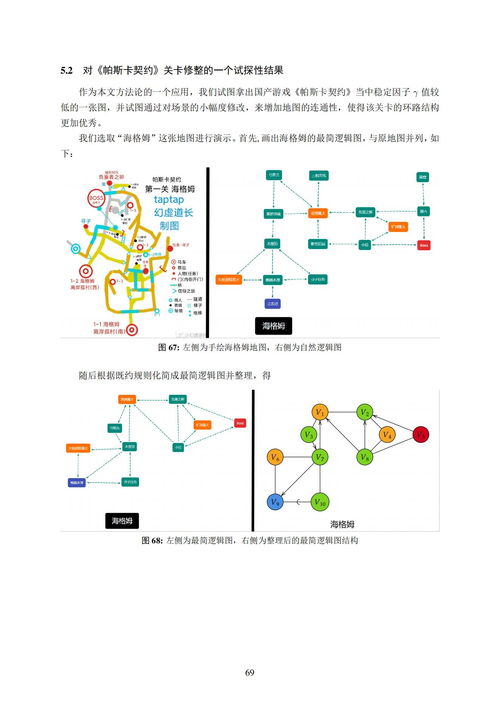
那么，拓扑游戏解法又是怎么一回事呢？其实，它就是利用拓扑学的原理来解决一些特定类型的问题。比如，我们经常在游戏中遇到的各种路径规划、资源分配等问题，都可以用拓扑游戏解法来尝试解决。

让我们以一个经典的拓扑游戏——“外星文字典”为例。在这个游戏中，你有一系列的外星文字符，它们之间存在着某种联系。你的任务是找出这些字符之间的顺序关系，从而解开这个外星文字典。

要解决这个问题，我们可以将每个字符看作一个节点，字符之间的联系看作是有向边。我们就可以利用拓扑排序的方法来找出字符之间的顺序。这种方法的关键在于，它能够帮助我们找到一种不违反任何联系关系的字符排列。

三、拓扑游戏解法的应用

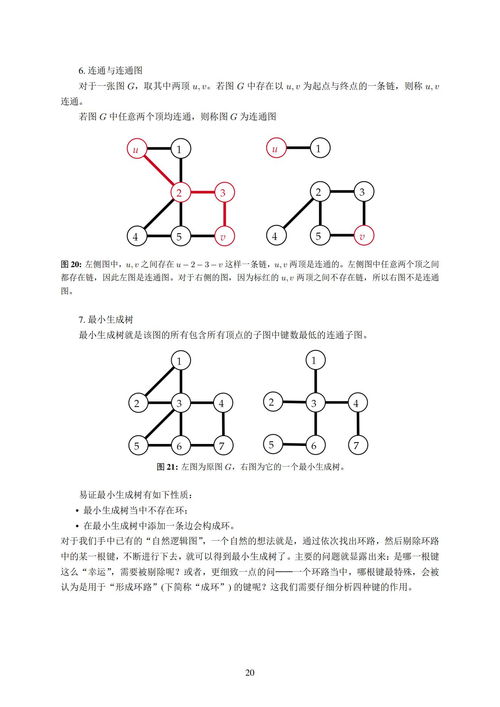
拓扑游戏解法不仅在游戏中有着广泛的应用，在现实世界中也有着重要的意义。比如，在计算机科学中，拓扑排序可以用来检测有向图中的环；在工程领域，它可以用来优化电路设计；在经济学中，它可以用来分析市场结构。

让我们再来看一个例子：在课程设计中，你可能会遇到这样的情况：有些课程是其他课程的先决条件。这时，你可以使用拓扑排序来找出课程的合理顺序，确保学生能够按照正确的顺序学习。

四、拓扑游戏解法的挑战

当然，拓扑游戏解法并不是万能的。它也有一些局限性。比如，它只适用于有向无环图（DAG图），也就是说，图中不能存在任何环。此外，拓扑排序的结果可能不是唯一的，也就是说，可能存在多种满足条件的字符排列。

那么，如何克服这些挑战呢？首先，我们需要对问题进行仔细的分析，确保它符合拓扑排序的条件。其次，我们可以尝试使用不同的算法来寻找最优解，比如多源BFS（广度优先搜索）。

五、拓扑游戏解法的未来

随着科技的不断发展，拓扑游戏解法将会在更多领域得到应用。比如，在人工智能领域，它可以用来优化算法；在生物信息学领域，它可以用来分析基因序列。

拓扑游戏解法是一种强大的数学工具，它可以帮助我们解决各种复杂问题。让我们一起期待，这个神奇的解法在未来会带给我们更多的惊喜吧！

亲爱的读者们，今天的数学之旅就到这里。希望你们在探索拓扑游戏解法的过程中，能够感受到数学的魅力。别忘了，数学的世界充满了无限可能，只要我们用心去发现，就能找到属于自己的精彩。下次再见！